Fluent中“case.out”数据导入Matlab并绘制曲线

  1. 将Matlab .m文件与 .out文件存储在同一文件夹下
  2. 直接运行 .m文件即可调用 .out文件中的数据并绘制曲线
  3. 以下例程是Fluent里面导出的搅拌桨扭矩和迭代步数的数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
clc
clear all
close all

% 提取出 .out文件中的数据，存放到数组data中
data = load('case.out');

% 将数组data赋值到x，y轴
x = data(:,1);
y = abs(data(:,2));

figure
plot(x,y'--');
xlim([0 1000]);
ylim([0 80]);
title('搅拌扭矩与迭代步数的关系');
xlabel('Number of Iterations');
ylabel('Torque of Stirring')
grid on;

Matlab GUI设计

暂无

Matlab基础

  1. Matlab 文件命名规则

  • 文件名命名要用英文字符，第一个字符不能是数字和下划线。

  • 文件名不要取为Matlab 的一个固有函数,m 文件名的命名尽量不要是简单的英文单词，最好是由大小写英文、数字、下划线等组成。原因是简单的单词命名容易与Matlab内部函数名同名，结果会出现一些莫名其妙的错误。

  • 文件存储路径一定为英文。

  • m 文件起名不能有空格，如three phase，应该写成three_phase 或者ThreePhase，推荐后者，因为C++ 也是这样命名的。

总结：matlab文件命名最主要的原则是第一个字符不能是数字和下划线，不能有空格。

  1. Matlab程序注意事项
  • Matlab语言区分大小写。Differ the uppercase and lowercase.
  • Matlab可以通过脚本文件和命令两种方式工作。The matlab can work by two ways of script file and command.
  1. Matlab清除命令
1
2
3
4
5
6
clc % 清除命令行窗口的内容
clf % 清除当前Figure
clear % 清除工作空间所有变量
clear all % 清除工作空间所有变量，函数，和MEX文件
close % 关闭当前绘图窗口（Figure）
close all % 关闭所有绘图窗口（Figure）

  1. Matlab数值运算 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    % 加减乘除
    a = 100;
    b= 20;
    sum = a + b %加法运算
    sub = a - b %减法运算
    mul = a * b %乘法运算
    div = a / b %除法运算

    % 向量矩阵运算
    ```Matlab
    % Vector(1×4)，定义列矢量
    x = [1 2 3 4]
    x = [1,2,3,4]
    % Matrix(2×2)
    x = [1,2;3,4]
    % 基于向量元素间距生成列向量
    x = [1:0.5:10]
    % 基于向量元素个数生成列向量，个数19。
    x = linspace(1,10,19)
    % 查找向量长度
    length(x)
    % 2×2“单位阵”
    E = eye(2)
    % 3×4“零阵”
    Z = zeros(3,4)
    % 3×4“全1阵”
    O = ones(3,4)
    % 3×4“随机阵”
    R = rand(3,4)
    % (1×3)×(3×3)=(1×3)
    x = [1,2,3]
    y = [2,3,4;4,5,6;6,7,8]
    x*y % 矩阵运算——乘法,计算行与列之间的内积
    x.*y % 数组运算——乘法,元素级乘法（而非矩阵乘法）
    x/y % 右除
    x = x' % 转置
    y\x % 左除
    pinv(y) % 求逆
    rank(y) % 求秩
    det(y) % 求行列式
    z = [10,11,12]
    a = [y;z] % 在矩阵y下方加上z
    a = [y [z;zeros(2,3)]] % 在矩阵y右边加上z，但由于结构不一致，需要进行矩阵填充。
    [row,col]=find(y==5)
    [V,D] = eig(A) % 求特征值、特征向量
    1
    2
    3
    4
    5
    6
    7
    % 方阵四则运算
    a= [1, 2; 3, 4];
    b= [5, 6; 7, 8];
    sum = a + b 
    sub = a - b
    mul = a * b 
    div = a / b
    1
    2
    3
    4
    5
    % 多项式表示
    % str2poly(): 实现从多项式的字符串表示转换为多项式的行向量表示，输入不必降幂排列，代码如下：
    str2poly('x^7-2x^6+3x^5-5x^4+x^2-1','x') % Matlab没有这个函数
    % str2poly(): 实现了把一个行向量表示的多项式转换为常见的字符串表示的多项式，代码如下：
    poly2str([1 -2 3 -5 0 1 0 -1],'x')

  2. Matlab符号运算 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    % 符号定义的几种形式
    syms a; % 符号
    a=sym('a'); % 符号，若括号内的a为常量，则称谓符号常量
    f1='3*x+4'; % 符号表达式，char类型，但是可以参与运算。所以这种形式是可以直接用的，比较方便

    % 符号表达式的化简
    syms x y
    s = (x^2+y^2)^2 + (x^2-y^2)^2;
    simplify(s);

    % 符号替代
    % Symbolic substitution，subs(s,old,new)
    syms x
    f1 = x^3 -9;
    subs(f1,3)

    % 因式分解、展开与合并同类项
    syms a b x y
    f1=a^3-b^3;
    factor(f1);

    f2=(3*x^2+8*y^2)*(-x^2+3*y);
    expand(f2)

    f3 = 2*x+3*x+4*x+y;
    collect(f3)

    % 极限实例
    syms x y; 
    y = sin(x) / x; 
    result = limit(y, x, 0)

    % 微分实例
    syms x y; 
    y= sin(x) / x; 
    result = diff(y, x, 1)

    % 积分实例
    syms x y;
    y =x * exp(x);
    result = int(y)

    % 级数求和（定级数、不定级数）
    % symsum(fun,var,a,b):其中fun是通项表达式，var为求和变量，a为求和起点，b为求和终点
    syms n;
    f1=1/(n*(2*n+1));
    I=symsum(f1,n,1,inf)

    % Taylor Series（泰勒级数）
    % taylor(fcn,x,x0,'Order',6);%对函数fcn在点x0处，进行6阶泰勒展开
    syms x
    f = 1/(5 + 4*cos(x));
    T = taylor(f, 'Order', 8)

  3. 方程求解 20220113170829 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    % 建立方程
    syms x
    eqn = sin(x) == cos(x);
    solve(eqn,x)

    % solve方程求解
    % Equations and systems solver，支持数值/符号求解，代数方程
    syms x
    eqn = sin(x) == 1;
    solx = solve(eqn,x)

    [x,y] = solve('x+y=10','x-y=2','x,y')  % 方程组求解，输出x和y的值

    % dsolve微分方程求解
    % Differential equations and systems solver，支持数值/符号求解，微分方程
    syms a y(t)
    eqn = diff(y,t) == a*y;
    dsolve(eqn)

    eqn = dsolve('2*D2x+Dx+6*x=0','Dp=-p-6*x','x(0)=1','Dx(0)=0','p(0)=0');
    x = eqn.x;
    p = eqn.p;

    % 非线性方程求解（数值解，非线性方程一般很难给出解析解）
    % Solve system of nonlinear equations
    function F = root2d(x) % 注意文件名与函数名一致
    F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
    F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
    end
    fun = @root2d;
    x0 = [0,0];
    x = fsolve(fun,x0)

  4. Matlab 绘图 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    % 实例1：绘制正弦曲线（使用的函数：plot）
    x = -10:0.1:10;
    figure(1)
    plot(x, sin(x));

    % 实例2：绘制余弦曲线
    x = -10:0.1:10;
    y = sin(x);
    figure(2)
    plot(x, y);

    % 实例3：同时绘制多个图形（使用函数hold on）绘制正余弦曲线
    x = -10:0.1:10;
    y1 = sin(x);
    y2 = cos(x);
    figure(3)
    plot(x, y1);
    hold on;
    plot(x, y2)

    % 实例4：设置曲线属性，曲线形状-颜色-数据点
    x = -6*pi:0.1:6*pi;
    y = sin(x);
    figure(4)
    plot(x,y, 'r--', 'linewidth', 2)

    % 实例5：设置坐标轴范围，使用的函数 axis
    x = 0:0.01:pi/2;
    figure(5)
    plot(x,tan(x), '-ro');
    axis([0 pi/2 0 50])
    grid on

    % 实例6：设置图形标识：legend函数，title函数，xlabel函数，ylabel函数，text函数等.
    x = -3*pi:0.1:3*pi;
    y1 = sin(x);
    y2 = cos(x);
    figure(6)
    plot(x, y1, 'r-');
    hold on
    plot(x, y2, 'b--')
    legend('sin(x)', 'cos(x)');
    axis([-12 12 -1.5 1.5])
    grid on

  5. 技巧

    1
    2
    3
    4
    % help “command”可以实现函数查找
    % 命令行窗口向上箭头可以查看以前的命令
    % "%%"可以对Matlab进行分块
    % 矩阵除法在Matlab里定义为矩阵求逆后相乘。例如矩阵右除B/A = B*inv(A)，矩阵左除A\B = inv(A)*B。

  6. 矩阵的运行结构 C语言中，if for while switch，Matlab类似。 

    1
    2
    3
    4
    5
    % 1-10的和
    sum = 0;
    for i = 1:10
        sum = sum+i;
    end
    1
    2
    3
    4
    5
    6
    7
    8
    % if条件语句  
    a = input('请输入a:');
    if a == 10
        a = a+1;
    else
        a = a-1;
    end
    disp(a); % 命令行窗口显示a的值

%%符号方程求解 %代数方程 clear syms x solve(x+x*exp(x)-10);

solve('x+xexp(x)-10') % 和前面的符号表达式方法联系起来了 eval(solve('x+xexp(x)-10')) % 这是数值的表达结果

% 方程组 [x,y] = solve('x+y=10','x-y=2','x,y') % 输出x和y的值

经典控制理论

  1. 系统模型形式

模型实例：

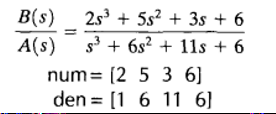
20211129235352

Numerator 分子；Denominator 分母；Residu 留数；Pole 极点；Direct item 直项；zero 零点。

模型有四种常见类型： - 传递函数基本分式形式：tf(num,den) - 20220226105558 - 部分分式形式：residue(num,den) - 零极点、增益形式：tf2zpk(num,den) - - 状态空间形式：tf2ss(num,den) -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
%清除命令窗口的内容
clc;
%关闭所有的Figure窗口
close all
%清除工作空间的所有变量，函数，和MEX文件
clear all;
%传递函数分子系数
num=[2 5 3 6];
%传递函数分母系数
den=[1 6 11 6];
%传递函数基本形式
sys=tf(num,den);
%传递函数部分分式形式
[r,p,k]=residue(num,den);
%传递函数：基本形式→零极点增益形式
[z,p,k]=tf2zpk(num,den);
%传递函数：基本形式→状态空间表达式形式
[A,B,C,D]=tf2ss(num,den);

%传递函数：零极点增益形式→基本形式
[num,den]=zpk2tf(z,p,k);
%传递函数：状态空间表达式形式→基本形式
[num,den]=ss2tf(A,B,C,D);


%两个不同的状态空间表达式形式→串联
[A,B,C,D]=parallel(A1,B1,C1,D1, A2,B2,C2,D2)；
%两个不同的状态空间表达式形式→并联
[A,B,C,D]=series(A1,B1,C1,D1, A2,B2,C2,D2)；
%两个不同的状态空间表达式形式→正反馈
[A,B,C,D]=feedback(A1,B1,C1,D1, A2,B2,C2,D2,1)；
%两个不同的状态空间表达式形式→负反馈
[A,B,C,D]=feedback(A1,B1,C1,D1, A2,B2,C2,D2)；
%状态空间表达式形式→单位反馈
[A,B,C,D]=cloop(A1,B1,C1,D1)；