%系统的单位阶跃响应 step(sys); %系统的脉冲响应 impulse(sys); %向量卷积运算——两个向量卷积，简单理解其实就是多项式乘法，可以将零极点增益形式的传递函数的分子和分母系数求出，即求得[num,den]。 den=conv([1 1],[4 1]); %绘制系统的Nyquist图 nyquist (sys); %绘制系统的Bode图 bode(sys); %判断系统的稳定性，通过极点（根）＜0判定。 roots (den)；

注：（1）若tf(num,den)函数后加“；”，则命令窗口不显示最终结果；反之则显示。推论：在运算结方程或者设定参数后面加分号，即可达到在命令窗口不显示结果的目的。（2）ans为代表没有定义变量的输出结果；如果变量有定义，那么就不会出现ans。ans为最后一个的输出值，后面的值会替换前面的值。（3）“[]”是矩阵标识符；“()”是函数标识符。（4）tf(num,den) ⇔printsys(num,den,'s') （5）zpk()和zp()都可以

2、求系统的传递函数Simulink图。

3、求系统的状态空间Simulink图。

Matlab里面的script和live-scrip

    在matlab2016a及以上的版本不建议安装notebook来编写实施脚本，以为之后的matlab里面会有live-script，他可以创建实施脚本，使脚本与方便操作。那么这个live script到底好在哪里？
    在以前我们可以在命令窗口中写代码，然后运行，但这个很简陋，因为历史命令（代码行）和运行输出都在同一个窗口中，现在代码和运行输出是分开的，方便查看运行过的命令，这和RStudio很类似。同时，不仅仅是代码编写，插入的纯文本、图片、超链接，整个live script可以作为一个博客、笔记一样使用，简直是高配版markdown！

    自matlab2016a版本以来，matlab多了创建实时脚本的功能。在未来版本中作为mupad的替代。其思想与mathcad相似，企图将文档与程序合二为一。就是在原有m文件上加了交互式图标，富文本功能和控件。格式为mlx。2016a以上版本都可打开，还可以输出为pdf等用于分享。

注意：matlab实时编辑器的各节变量还是全局的，只是可以单节单独运行，而且live-script显示公式的可读性更强，也就印证了将文本和编程统一的思想。

MATLAB符号工具箱

syms R1 R2 L C V2 V1 s;
eqns = [V1/R2 == (V2 - V1)/(L*s + R1) + (V2 - V1)*s*C]; % representing the equation I1 = I2 + I3 using their exact expressions
V2tmp = solve(eqns, V2); % Here I am solving for the above equation for the variable "V2"
 TF = simplify(V2tmp/V1) % this step is computing the transfer function and calling the "simplify" on the result

matlab新建脚本和新建实时脚本的区别实时脚本不需要保存即可运行呢！但是有时候运算过程会卡顿

建议新建脚本，需要先保存才能运行，且保存文件可供后续的使用

符号变量定义sym、syms；

Simplify (J1)

pretty(f) 将符号表达式化简成与高等数学课本上显示符号表达式形式类似 collect(f) 合并符号表达式的同类项 horner(f) 将一般的符号表达式转换成嵌套形式的符号表达式 factor(f) 对符号表达式进行因式分解 expand(f) 对符号表达式进行展开 simplify(f) 对符号表达式进行化简，它利用各种类型的代数恒等式，包括求和、积分、三角函数、指数函数以及 Bessel 函数等来化简符号表达式 simple(f) 对符号表达式尝试多种不同的算法进行化简，以显示长度最短的符号表达式简化形式 % [r,how]=simple(f) 返回的 r为符号表达式进行化简后的形式， how为所采用的简化方法

matlab里面“；”代表矩阵一行的结束，而“，”表示一行的各个量。

func1=eliminate([Mdiff(x,t,2)==F-N-bdiff(x,t,1); N==mdiff(x+lsin(phi),t,2)], N) 等价于 eqns=[Mdiff(x,t,2)==F-N-bdiff(x,t,1), N==mdiff(x+lsin(phi),t,2)] func1=eliminate(eqns, N)

eliminate(eqns,vars) eqns：等式向量 vars：变量向量

MATLAB符号变量表达式与方程求解

主要内容 1. 符号计算基础 1.1 符号常量和符号变量语法： % 符号变量两种表达方式 sym a ;

            % 符号常量
                sym 3;
            
            %符号表达式
                sym x
                f=3*x+6;
                
    1.2 符号四则运算
        + - * / ^
        
    1.3 符号表达式的简化
            syms x y
            s = (x^2+y^2)^2 + (x^2-y^2)^2;
            simplify(s);
        
        % 因式分解、展开与合并同类项
            syms a b x y
            f1=a^3-b^3;
            factor(f1); % 因式分解
            
            f2=(3*x^2+8*y^2)*(-x^2+3*y);
            expand(f2); % 因式展开
            
            f3 = 2*x+3*x+4*x+y;
            collect(f3); % 因式合并同类项
            
    1.4 符号矩阵运算
        % 符号矩阵
            a1=[x x+y;y x+y];
            transpose(a1) % 转置
            
        % 符号函数值的求解
            syms x
            f1 = x^3 -9;
            subs(f1,3) % 赋值函数，用数值替代符号变量替换函数
            
2. 符号函数
    2.1 极限
        % 符号极限、符号微分、符号积分
            sym x
            y=sin(x);
            limit(y,0)
    
    2.2 微分
        % 符号极限、符号微分、符号积分
            sym x
            y1 = x^2;
            diff(y1)    % 求导、微分
            diff(y1,2) % 二阶导数
    
    2.3 积分
        % 符号积分
            sym x
            y3=(3-x^2)^3;
            int(y3)   % 不定积分
            y4=abs(1-x); % 绝对值函数
            int(y4,1,2)   % 定积分1-2范围内
    
3. 符号级数

4. 符号方程求解
    4.1 代数方程
        %代数方程
            clear all
            syms x
            solve(x+x*exp(x)-10);
            eval(solve(x+x*exp(x)-10)) % 这是数值的表达结果
        
        %方程组
            [x,y] = solve('x+y=10','x-y=2','x,y')  % 输出x和y的值
        
    4.2 微分方程
        % 符号的微分方程
            dsolve('Dy-(x^2+y^2)/x^2/2','x')  
        % 微分方程组合上面的方程组道理一样

syms是定义符号变量；sym则是将字符或者数字转换为字符。

y=sym('x');与 syms x; y=x; 的功能一样。另外sym x和syms x有很大的区别： sym x是将字符'x'转换为字符，而syms x则是定义符号变量x。

clear all

syms x solve(x+x^2-10==0,x)

clear all syms x solve(x+x^2-10,x)

clear all syms x solve(x+x^2-10)

%显示错误 clear all sym x solve(x+x^2-10==0,x)

clear all

syms x solve(x+x^2-10==0,x)

clear all syms x solve(x+x^2-10,x)

clear all syms x solve(x+x^2-10)

%显示错误 clear all sym x solve(x+x^2-10==0,x)

Matlab符号工具箱使用简介

一、符号对象的创建二、微积分基本运算三、解方程四、符号表达式的化简和代换五、符号函数曲线的绘制

一、符号对象的创建在数学应用中，常常需要做极限、微分、求导数等运算，MATLAB称这些运算为符号运算。 MATLAB的符号运算是通过调用符号运算工具箱（Symbolic Math Toolbox）内的工具实现，其内核是借用Maple数学软件的。MATLAB的符号运算工具箱包括微积分运算、解方程、线性代数、化简和代换等几个方面的工具。符号运算工具箱处理的主要对象是符号对象，包括符号、符号变量和符号表达式。

字符串变量的创建用单引号界定的字符序列称为字符串。字符串是一种特殊的符号对象，在数据处理、造表和函数求值中，字符串具有重要的应用。

例1 >>s = 'hello' s = Hello

【注】①字符串中的字符可以是数字、英文字母、汉字、横线、括号、表达式等。 ②用赋值符号“=”把字符串赋给某个标识符，例如s，这个标识符称为字符串变量名，简称字符名。

2.符号变量、表达式的创建 MATLAB中有两个函数定义符号变量、表达式（1）sym函数调用格式：f=sym('表达式') 功能：用于生成单个的符号对象。

例2： >>sym('x') ans = x % 符号变量 >>y = sym('2+cos(x)') y = 2+cos(x) % 三符号表达式

（2）syms函数调用格式：syms varl var2 var3 … [flag] 功能：用于生成多个符号对象，注意空格。其中flag指定符号变量的类型：real，unreal

例3： >>syms y u %两个符号变量 >>p = exp(-y/u) p = exp(-y/u) % 符号表达式 >>q = y^2+u3+uy q = y^2+u3+uy % 符号表达式

3.符号表达式中的符号变量的确认调用格式：findsym（“表达式”）功能：用于确定一个表达式中的符号变量例4： >>syms a b c k t y real >>g=q+a(2p-1)^3-bsin(4y) g=y^2+u3+uy+a(2exp(-y/u)-1)^3-bsin(4*y) >>findsym(g) % 找出所有的符号变量 ans=a, b, u, y >>findsym(g, 2) % 找出距x最近的2个符号变量 ans=y, u

4.将符号表达式结果转化为数值调用格式：double('表达式') 功能：将符号常数转化为双精度数值例5 考察符号对象和普通数据对象之间的差别： >>sqrt(2) % 返回数值结果 ans = 1.4142

x = sqrt(sym(2)) % 返回符号结果 x = 2^(1/2) double(x) % 符号常数转化 ans = 1.4142

二、微积分基本运算设a, b, t, x, y是已定义的符号变量 1. 求极限调用格式：limit(f, x, a [, 'right/left']) 功能：求f表达式在x->a时的极限（单侧极限）

例1 求极限lim_(x→2)⁡〖(x−a)/(x^2−a2 )〗 >>syms x a >>f = (x-a)/(x^2-a2)； >>limit(f, x, 2) % 求x>2时的极限 ans=1/(2+a) >>limit(f, a, 2) % 求a > 2时的极限 ans = 1/(x+2) >>limit(f) % 默认x > 0 ans = l/a >>limit(1/x) % 求x > 0时极限不存在 ans = NaN >>limit(1/x, x, 0, 'left') % 左极限 ans = -inf >>limit(1/x, x, 0, 'right') % 右极限 ans = inf

求导数（注意diff具有求导和求差分两种功能，特别注意''的使用）符号微分和数值微分调用格式：diff(f, v, n) 功能：对指定变量v求n阶导数

例2 求导数 >>syms x a t; f = sin(ax)-cos(at); >>g1 = diff(f) % 默认对x求导 g1 = cos(ax)a >>g2 = diff(f, a) % 对a求导 g2 = coa(ax)x+sin(at)t >>g3 = diff(f, x, 2) % 对x求二阶导数 g4 = -sin(ax)a^2

例3 对符号矩阵求导, 是作用于矩阵的每个元素 >>syms x a t; >>A = [sin(ax), cos(tx); a^2-xt, t^2+tx] A = [sin(ax), cos(tx)] [a^2-xt, t^2+tx] >>dy = diff(A) % 默认对x求导 dy = [cos(ax)a, -sin(tx)t] [-t, t] >>dy = diff(A, t) % 对t球导 dy = [0, -sin(tx)x] [-x, 2*t+x]

求积分调用格式：int(f, v, [a, b]) 功能：对f表达式的v变量求定积分(在区间[a, b]求定积分)

例4 求不定积分 >>syms x a t; >>f = sin(ax); g = int(f) % 默认对x求积分 g = -1/acos(ax) >>g=int(f, a) % 对a求积分 g = -1/xcos(a*x)

例5 求定积分 >>syms x a t; >>f = sin(ax); g = int(f, 0, pi) % 对x求定积分 g = -(cos(pia)-1)/a >>f = sin(ax); g = int(f, a, 0, pi) % 对a求定积分 g = -(cos(pix-1)/x >>f = exp(-x^2); g = int(f, 0, 1) % 结果无解析表达式 g = 1/2erf(1)pi^(1/2) >>a = double(g) a = 0.7468 % 求定积分数值

级数求和调用格式：symsum(f, t, a, b) 功能：对f表达式的符号变量t从a到b求级数和

例6 计算级数 >>syms x n >>symsum(1/x, 1, 3) ans = 1l/6 >>S1 = symsum(1/x^2, 1, inf) Sl = 1/6*pi2 >>S2 = symsum(x^n, n, 0, inf) S2 = -l/(x-1)

泰勒级数展开调用格式：taylor(f, n, x, a) 功能：函数f自变量x在a点展开n-l次泰勒多项式 f(x)=∑24_(k=0)^(n−1)▒(f((k) ) (a))/k! 〖(x−a)〗^k

例7 泰勒展开 >>syms x; f = sin(x); >>taylor(f) % f在x = 0点的5次泰勒多项式 ans = x-1/6x^{3+1/120x^5 >>taylor(f,
4, [], 2) % f在x = 2点的3次泰勒多项式 ans =
sin(2)+cos(2)(x-2)-1/2sin(2)(x-2)}2-1/6cos(2)*(x-2)^3

三、解方程 1. 非线性方程(组) 调用格式：S = solve(fl, f2, …, fn, xl, x2, …, xn) 功能：求方程组fl, …, fn关于指定变量xl, …, xn的解

例1 解方程(组) >>syms a b c x; f = ax^2+bx+c; % f中无等号 >>s = solve(f) % 解方程f = 0 S = [1/2/a(-b+(b^2-4a*c)(1/2))] [1/2/a(-b-(b^2-4a*c)(1/2))]

例2. 解非线性方程(组) >>syms x y; >>fl = 'x2+xy+y = 3'; % 方程用单引号括起 >>f2 = 'x^2-4*x+3 = 0'; >>[x, y] = solve(fl, f2, x, y)

syms x y; fl = x2+xy+y == 3; % 方程用单引号括起 f2 = x^2-4*x+3 == 0; [x, y] = solve(fl, f2, x, y)

x = [1] [3] y = [1] [-3/2] 方程组的解为：(1, 1)和(1, -3/2)

微分方程(组) 调用格式：dsolve ('S', 'sl', 's2', …, 'x') 功能：解微分方程组S, 初始条件为sl, s2, …, 自变量x 【注】①默认的自变量为t. ②方程中用D表示微分, 如Dy表示; 如果在D后面带有数字, 则表示多阶导数, 如D2y表示; ③如果不指定初始值, 或者初始值方程的个数少于因变量的个数, 则最后得到的结果中会包含常数项, 表示为C1, C2等. ④dsolve函数最多接受12个输入参数

例3 解微分方程 >>syms x y >>dsolve('Dy = 1+y^2') ans = tan(t+Cl) % 默认自变量为t, 包含常数Cl >>y = dsolve('Dy = l+y^2', 'y(0) = 11', 'x') % 指定初值 y = tan(x+1/4pi) >>x = dsolve('D2x+2D1x+2x = exp(t)', 'x(0) = 1', 'Dx (0) = 0') % 二阶微分方程, 指定初值 x = 1/5exp(t)+4/5exp(-t)cos(t)+3/5exp(-t)sin(t)

例4 解微分方程组 >>syms f g >>S = dsolve('Df = 3f+4g', 'Dg = -4f+3g') S = f: [1×l sym] g: [1×l sym] % 返回结构数组S >>f = S.f, g = S.g % 查看s中f, g的值 f = exp(3t)(cos(4t)C1+sin(4t)C2) g = exp(3t)(-sin(4t)Cl+cos(4t)C2)

线性代数给定线性方程组{■8(■8(a_11 x_1+a_12 x_2+⋯+a_1n x_n=b_1@a_21 x_1+a_22 x_2+⋯+a_2n x_n=b_2@⋮)@a_n1 x_1+a_n2 x_2+⋯+a_nn x_n=b_n ) ┤ 设A =(■8(■8(■8(a_11&a_12&⋯@a_21&a_22&⋯@⋮&⋮&⋱)@■8(a_n1&a_n2&⋯))&■8(■8(a_1n@a_2n@⋮)@a_nn ))) , A =(■8(■8(x_1@x_2@⋮)@x_n )), b =(■8(■8(b_1@b_2@⋮)@b_n )), 按矩阵乘法, 线性方程组(1)可表示为 Ax=b

基本命令： Ax=b ①求非齐线性方程组Ax = b的(特)解：x = A求齐次线性方程组Ax = 0的基础解系：X = null(A) ③求矩阵A的特征值：[V, L] = eig(A) ④求方阵A的行列式：D = det(A)

例5 解线性方程组 >> syms a b c; A = [a b c; b c a; c a b]; B = [1 1 1]; >> X = A X = [1/(a+c+b)] [1(a+c+b)] [1/(a+c+b)]

例6 解线性方程组 > A = sym([1 1 -3 -1; 3 -1 -3 4; 1 5 -9 -8]); % 符号化矩阵 >> b = sym([1 40]); >> Xl = A X = nul(A) 特解X1 = [5/4] [-1/4] [0] [0] 基础解系 X = [-3/4, 3/2] [7/4, 3/2] [0, 1] [1, 0] >>syms kl k2 >> k = [k1; k2]; >> XX = Xl+X*k 通解 XX = [5/4-3/4+k1+3/2*k2] [-1/4+74k1+3/2k2] [k2] [kl]

四、符号表达式的化简和代换 1. 化简符号表达式 MATLAB提供了许多化简符号表达式的函数： ①合并同类项(降幂排列)：collect(P, x) ②将乘积展开为和式：expand(P) ③把多项式转换为嵌套形式：horner(P) ④多项式因式分解：factor(P) ⑤利用各种恒等式化简：simplify(P) ⑥用习惯书写方式显示：pretty(f)

例1 合并同类项, 将乘积展开 >> symc x y t >> collect(x^{3+2x^2-5x}2+4+x-3x+12-3) % 合并同类项 ans = x^{3-3x^2+x+9 >> g = collect(1+x)t+tx) %
合并同类项 g = 2tx+t >>
expand((x-1)(x}2)(x-3)) % 乘积展开 ans = x^3-6x^2+11x-6 >> expand(cos(x+y)) % 乘积展开 ans = cos(x)cos(y)-sin(x)sin(y)

例2 转换为嵌套形式, 因式分解 >> horner(x^3-6x^{2+11x-6) % 转换为嵌套 ans =
-6+(11+(-6+x)x)x >> P = horner(1.1+2.2x+3.3x^2)
% 转换为嵌套 P = 11/10+(11/5+33/10x)x >>
factor(x^3-6x}2+11x-6) % 因式分解 ans = (x-1)(x-2)(x-3) >> n-1: 5; X = [x, x, x, x, x]; P = x^n+l P = [1+x, x^2+1, x^3+1, x^4+1, x^5+1] > >f = factor(P) % 因式分解 f = [l+ x, x^2+1, (1+x)(x^2-x+1), x^4+1, (1+x)(x^4-x3+x^2-x+1)]

例3. 恒等式化简, 习惯书写方式 >>syms x y a b >>q = simplify((1-x^3)/(1-x)) % 化简符号表达式 q = x^2+x+1 >> p = simplify(a^3+6/a2+12/a+8S)^(1/3)) p= ((2*a+1)^3/a3)^(1/3) >> pretty(P) % 习惯书写方式显示 (■8(3@(2a+1))/■8(3@a))^(1∕3)

代换命令 MAILAB提供了两种代换命令：

A = subs(S, old, new) 用符号new置换表达式S中的符号old, 得到A
A = subexpr(S, ss) 用符号变量置换表达式S中的公共子表达式, 得到A

例4 符号置换 >> syms a b c x y, A = subs(a^2+2ab+b2, a, 4) A = 16+8*b+b^2 >> B = subexpr(a^2+2ab+b2, a, x) B = x^2+2xb+b2

例5 符号置换 >> syms a b c d w; >> A = [a b; cd]; (V, D] = eig(A); >> [RVD, W] = subexpr([V; D], W) RVD = [-(1/2d-1/23-1/2W)c, -(1/2d-1/2a+1/2W)/c] [1, 1] [1/2+d+1/2+a+1/2+W, 0] [0, 1/2d+1/23-1/2W] w = (d^2-2ad+a2+4bc)^(1/2)

五、符号函数曲线的绘制 MATLAB提供了绘制符号的数曲线命令： (1) ezplot(f, [min, max]) 绘制函数f在指定区间内的2维曲线图 (2) ezplot3(x, y, z, [tmin, tmax]) 在指定参数区间内绘制3维曲线图 (3) ezmeshc(f, domain) 绘制二元函数f在指定区域上的图形, domain为4×1数组

erf函数

在数学中，误差函数（也称之为高斯误差函数，error function or Gauss error function）是一个非基本函数（即不是初等函数），其在概率论、统计学以及偏微分方程和半导体物理中都有广泛的应用。

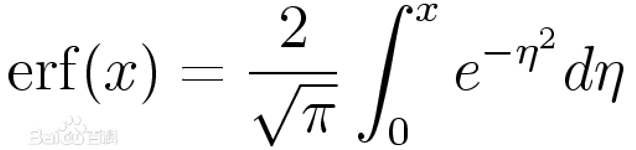
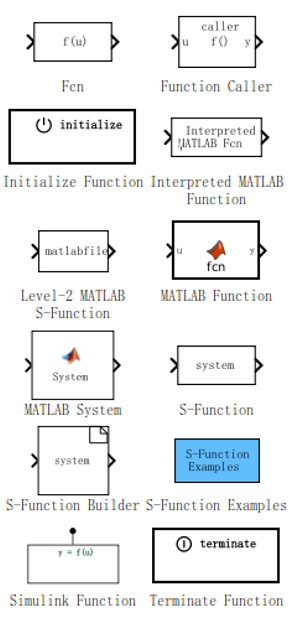
Simulink/User-Defined Functions

20211130000339 Fcn：（在 R2006a 之前推出）Fcn 模块将指定的数学表达式应用于其输入。表达式可以包含以下一个或多个组成部分： u - 模块的输入。如果 u 是向量，则 u(i) 表示向量的第 i 个元素；u(1) 或单独一个 u 表示第一个元素。数值常量。算术运算符 (+ - * / ^)。关系运算符 (== != > < >= <=) - 如果关系为 true，表达式返回 1；否则返回 0。逻辑运算符 (&& || !) - 如果关系为 true，表达式返回 1；否则返回 0。括号。数学函数- abs、acos、asin、atan、atan2、ceil、cos、cosh、exp、floor、hypot、log、log10、power、rem、sgn（等效于 MATLAB® 中的 sign）、sin、sinh、sqrt、tan 和 tanh。

Function Caller：Function Caller 模块调用并执行使用 Simulink® Function 模块定义的函数或导出的 Stateflow® 函数。使用 Function Caller 模块，您可以从模型或图形层次结构中的任意位置调用函数。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

Initialize Function：Initialize Function 模块是预配置的子系统模块，它在发生模型初始化事件时执行。默认情况下，Initialize Function 模块包括一个 Event Listener 模块（其 Event 设置为 “Initialize”）、一个 Constant 模块（其 Constant value 设置为 0）和一个 State Writer 模块。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

Interpreted MATLAB Function：（在 R2011a 中推出）Interpreted MATLAB Function 模块用于将指定的 MATLAB® 函数或表达式应用于输入。函数的输出必须与模块的输出维度相匹配。此模块很慢，因为它在每个积分步中都会调用 MATLAB 解析器。请考虑改用内置模块（如 Math Function 模块）。或者，您可以编写 MATLAB S-Function 或 MEX 文件 S-Function 形式的函数，然后使用 S-Function 模块访问该函数。

MATLAB Function（在 R2011a 中推出）：使用 MATLAB Function 模块可以编写用于 Simulink® 模型的 MATLAB® 函数。您创建的 MATLAB 函数针对仿真执行，并生成以 Simulink Coder™ 为目标的代码。扩展功能 C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。 HDL 代码生成，使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 Verilog 代码和 VHDL 代码。 PLC 代码生成，使用 Simulink® PLC Coder™ 生成结构化文本代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

Level-2 MATLAB S-Function：（在 R2010b 中推出）此模块允许您在模型中使用 Level-2 MATLAB® S-Function。为此，请在模型中创建此模块的实例。然后，在模块参数对话框的 S-function name 字段中输入 Level-2 MATLAB S-Function 的名称。使用 S-Function 模块在模块中包含 Level-1 MATLAB S-Function。如果 Level-2 MATLAB S-Function 定义了其他参数，您可以在模块参数对话框的 Parameters 字段中输入它们。将参数输入为 MATLAB 表达式，以按照 MATLAB S-Function 定义的顺序计算它们的值。使用逗号分隔每个表达式。如果模型中包含 Level-2 MATLAB S-Function 模块，而 S-Function 中发生错误，则 Level-2 MATLAB S-Function 模块将在对话框中显示该错误的 MATLAB 堆栈跟踪信息。点击 OK 关闭此对话框。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

注意：提供Level-1 MATLAB文件S函数是为了确保具有先前S函数的Simulink模型能够正确仿真。使用Level-2 MATLAB文件S函数来开发新的S函数。

MATLAB System：（在 R2013b 中推出）MATLAB System 模块将现有的 System object（基于 matlab.System）添加到 Simulink® 中。它还允许您使用 System object API 为 Simulink 开发新模块。对于解释执行，模型使用 MATLAB® 执行引擎进行模块仿真。对于代码生成，模型使用代码生成进行模块仿真（使用代码生成支持的 MATLAB 代码子集）。MATLAB System 模块仅支持 MATLAB 中的部分可用函数。扩展功能 C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。 HDL 代码生成，使用 HDL Coder™ 为 FPGA 和 ASIC 设计生成 Verilog 代码和 VHDL 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

S-Function（在 R2006a 之前推出）：通过 S-Function 模块，可以从模块图中访问 S-Function。由 S-function name 参数指定的 S-Function 可以是 Level-2 MATLAB® S-Function，也可以是 Level-1 或 Level-2 C MEX S-Function。使用 Level-2 MATLAB S-Function 模块，在模块图中包含一个 Level-2 MATLAB S-Function。S-Function 模块显示指定的 S-Function 的名称，以及该 S-Function 指定的输入和输出端口的数量。连接输入端口的信号必须具有 S-Function 为输入端口指定的维度。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

S-Function Builder（在 R2006a 之前推出）：S-Function Builder 集成新的或现有 C 或 C++ 代码，并根据您提供的设定创建 C MEX S-Function。S-Function Builder 模块实例还作为 Simulink® 模型中生成的 S-Function 的封装程序。在仿真包含 S-Function Builder 模块实例的模型时，Simulink 软件调用生成的 S-Function，以调用该实例的mdlStart、mdlOutputs、mdlDerivatives、mdlUpdate 和 mdlTerminate 方法中您的 C 或 C++ 代码。S-Function Builder 模块不支持封装。但是，您可以封装包含 S-Function Builder 模块的 Subsystem 模块。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

S-Function Examples：一些实例。

Simulink Function（在 R2014b 中推出）：Simulink Function 模块是一个预先配置的 Subsystem 模块，可以用它作为一个起点来使用 Simulink® 模块以图形方式定义函数。该模块为函数调用方提供了文本接口。您可以从 Function Caller 模块、MATLAB Function 模块或 Stateflow® Chart (Stateflow) 调用 Simulink Function 模块。您可以在 Sequence Viewer 中可视化 Simulink Function 调用。该查看器可显示使用参数进行调用的时间和返回的值。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

Terminate Function：该终止功能块是预先配置的子系统块上的模型执行终止事件。默认情况下，“ 终止功能”块包括一个“ 事件侦听器”块，其中“ 事件”设置为Terminate，“ 终止符”块和一个“ 状态读取器”块。扩展功能： C/C++ 代码生成，使用 Simulink® Coder™ 生成 C 代码和 C++ 代码。定点转换，使用 Fixed-Point Designer™ 设计和仿真定点系统。

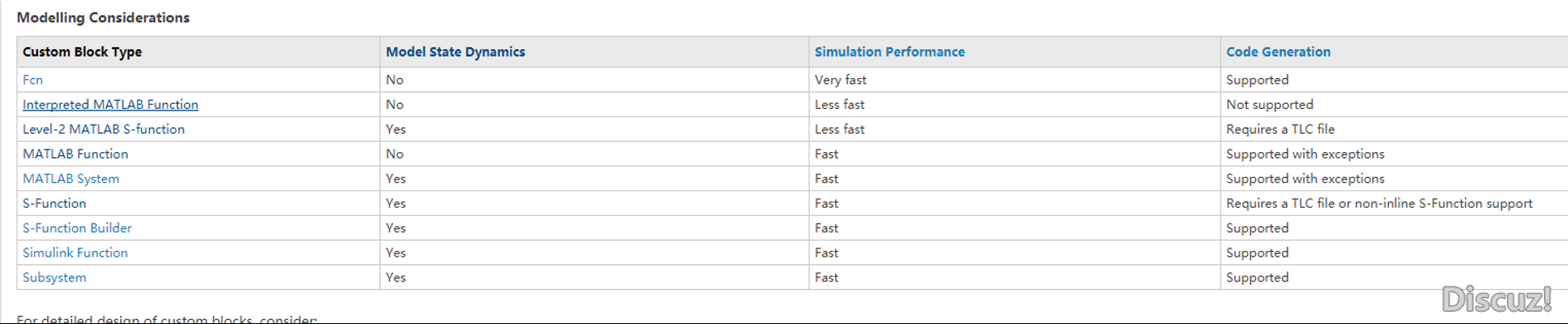
User-Defined Functions 自定义函数模块，如 MATLAB Function、MATLAB System、Simulink Function 和 Initialize Function

Simulink 模块 Argument Inport Simulink Function 模块的参数输入端口 Argument Outport Agument output port for Simulink Function block Event Listener Add event port to a subsystem block Fcn 对输入应用指定的表达式 Function Caller 调用 Simulink 或导出的 Stateflow 函数 Initialize Function Executes contents on a model initialize event Interpreted MATLAB Function 将 MATLAB 函数或表达式应用于输入 Level-2 MATLAB S-Function 在模型中使用 Level-2 MATLAB S-Function MATLAB Function 将 MATLAB 代码包含在生成可嵌入式 C 代码的模型中 MATLAB System 在模型中包含 System object Reset Function Executes contents on a model reset event S-Function 在模型中包含 S-Function S-Function Builder 集成 C 或 C++ 代码以创建 S-Function Simulink Function 使用 Simulink 模块定义的函数 State Reader Read a block state State Writer Write to a block state Terminate Function Execute contents on a model terminate event

Simulink中有以下几种用户自定义的函数模块： Fcn：适用于简单的表达式。所谓简单，不一定是表达式很短小，而是指输入输出之间的关系可以直接用一个表达式描述，即不使用状态，也不使用流程控制，而且需要注意，表达式中可用的函数比较有限（基本上就是一些简单的数学函数）。可以生成C代码。

MATLAB Fcn：很多人可能更容易掌握这个模块，这个模块对应一个M文件，对输入信号可以进行任何处理后得到输出。可以使用MATLAB的任何函数。限制主要有两个方面：（1）不能进行代码生成，所以准备做控制原形或半实物仿真的要尽量避免使用；（2）原则上不能使用状态量，也就是说，只使用当前时刻的输入经计算处理得到输出，而不能使用前一时刻的信息——如果需要使用前一时刻的信息，一般需要配合使用外部其他模块（如积分器或单位延时）。

Embedded MATLAB Fcn：和MATLAB Fcn类似，区别主要有以下几个方面：（1）可以生成C代码；（2）要求比MATLAB Fcn严格很多，而且有很多函数或工具箱在EMF中不允许使用（因为代码生成的限制）；（3）模块自身支持多输入多输出。function [output1, output2, output3...] = fcn_name(input1, input2, input3...)

S-Function：这是Simulink自定义模块最难掌握也是最强大的一种，原则上可以用它实现Simulink任何模块的功能。S函数与前几种模块的最大区别是可以使用状态，其根据仿真过程把代码分成几个部分：初始化、计算导数（积分由Simulink系统完成）、更新状态、计算输出、终止处理（其中中间几个是在仿真过程中周期性调用的），这给了用户以非常大的自由来进行代码的组织。S函数可以用C语言或M语言实现，而M语言又分不同的Level。写S函数有相应的模板和示例，想学的话需要花上一些时间才能搞明白。